1、
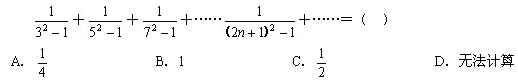
2、设“*”的运算法则如下:对任何若a+b≥10,则a*b=a+b;若a+b<10,则a*b=ab。则(1*2)+(2*3)+(3*4)+(4*5)+(5*6)+(6*7)+(7*8)+(8*9)+(9*10)=()
A.125 B.115 C.105 D.120
3、已知公差为2的正整数等差数列为an,则该数列满足不等式
A.12320 B.12430 C.12432 D.12543
4、一根长200米的绳子对折三次后从中间剪断,最后绳子的段数是()
A.8 B.9 C.11 D.16
5、在999张牌上分别写上数001,002,003,……,998,999。甲、乙两人分这些纸牌,分配方法是:凡纸牌上写的三位数字的三个数码都不大于5的纸牌属于甲,凡牌上有一个或一个以上的数码大于5的纸牌属于乙。例如,324,501等属于甲,而007,387,923等属于乙,则甲分得牌的张数为()
A.215 B.216 C.214 D.217
安徽公务员考试网(http://www.anhuigwy.org/)参考答案解析 题目或解析有误,我要纠错。
1.
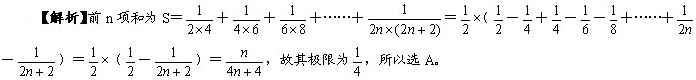
2【解析】B。(1*2),(2*3),(3*4),(4*5)都满足a+b<10,所以按a*b=ab计算,(5*6),(6*7),(7*8),(8*9),(9*10)都满足a+b≥10,所以按a*b=a+b计算,即:
(1*2)+(2*3)+(3*4)+(4*5)+(5*6)+(6*7)+(7*8)+(8*9)+(9*10)
=2+6+12+20+11+13+15+17+19
=115。故选B。
3【解析】A。公差为2的正整数数列为奇数列,满足条件的an最小为3,最大为221,故和为(3+221)×[(221-3)÷2+1] ÷2=12320。故选A。
4【解析】B。对折3次后是8根,从中间剪断后多16个头,加上原来绳子的2个头,总计18个头,2个头一线段,所以有18÷2=9段,故选B。
5【解析】A。所有三位数字的三个数不大于5的数总共有:6×6×6=216个,除去000,故甲分得的牌的张数为216-1=215张。故选A。










